Методы, которые созданы для построения и анализа DL- и AR-моделей, можно использовать для верификации макроэкономических моделей, учитывающих определенные ожидания относительно значений экономических показателей, включенных в модель в момент времени t. Рассмотрим модель адаптивных ожиданий вида

.

Здесь yt – фактическое значение результативного признака (объясняемой переменной), а – ожидаемое значение факторного признака в момент t+1.

Механизм формирования ожиданий в этой модели следующий:

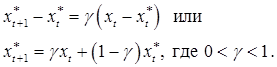
Таким образом, ожидаемое значение фактора в некоторый момент времени t+1 представляет собой средневзвешенную величину его фактического и ожидаемого значений в период времени t. Видно, что в каждый период t+1 ожидания корректируются на некоторую долю от разности между фактическим и ожидаемым значениями фактора в предыдущий период t. Параметр называют коэффициентом ожиданий. Чем ближе он к единице, тем в большей степени реализуются ожидания в отношении переменной yt, и наоборот, приближение коэффициента к нулю свидетельствует об устойчивости существующих тенденций экономического процесса. Это означает, что условия, преобладающие сегодня, будут сохраняться и на будущие периоды времени.

В уравнение подставим выражение и получим

. (*)

Далее, если рассматриваемая изначально модель имеет место для момента или периода t, то она, очевидно, будет действовать и в период t–1, а значит, мы можем записать: . Умножим последнее уравнение на и вычтем из уравнения (*):

.

Теперь мы можем определить параметры последнего авторегрессионного уравнения и легко перейти к исходной модели. По найденному в результате регрессионного анализа коэффициенту отыскивается коэффициент , по коэффициенту при отыскивается коэффициент b, а по свободному члену отыскивается свободный член исходного уравнения a.

Различие между начальным и последним уравнениями состоит в том, что первая модель включает в себя ожидаемое значение фактора , и к ней нельзя применять классические статистические методы. Последняя же модель включает в себя только фактические, то есть наблюдаемые значения переменных, и ее параметры можно определить.

Однако, как и в случае с моделью Койка, применение классического МНК приведет к смещению оценок параметров ввиду наличия в правой части лагового значения результативного признака .