Параметры модели в классическом варианте оценивают с помощью МНК. Предпосылки для МНК в множественной регрессии:

1) математическое ожидание остатков во всех наблюдениях равняется нулю ;

2) отсутствие гетероскедастичности остатков

;

3) отсутствие автокорреляции в остатках

;

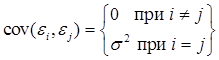4) объясняющие переменные детерминированы, а у – объясняемая переменная – случайна, и остатки не коррелируют с объясняющими переменными:

5) остатки должны быть распределены нормально:εi ~ N (0; σ);

6) регрессионная модель должна быть линейна относительно параметров;

7) отсутствие интеркорреляции и мультиколлинеарности

Уравнение множественной регрессии выглядит следующим образом:

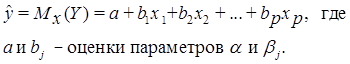
Обратившись к матричной форме записи, можно увидеть, что система нормальных управлений (СНУ) для такой множественной линейной модели будет иметь такой вид:

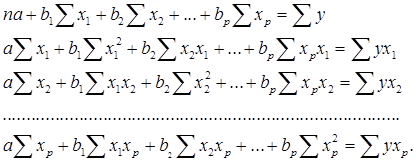
В матричной форме вектор оценки параметров запишется:

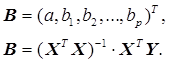
Дисперсия остатков отыскивается так:

Эти формулы справедливы для классического МНК при гомоскедастичности остатков и отсутствии автокорреляции в остатках.

Модель, где все факторы присутствуют в масштабах своих единиц измерения, не позволяет сравнить (оценить) степень вклада каждого фактора в результат, поэтому для исключения этого недостатка строят уравнения с использованием стандартизованных переменных и коэффициентов.

Коэффициенты регрессии такой модели имеют тот же смысл, что и в парной регрессии, только каждый коэффициент отвечает за свой фактор. Они показывают на сколько своих СКО изменится в среднем результат y, если соответствующий фактор изменится на одно свое СКО при неизменном среднем уровне остальных факторов.

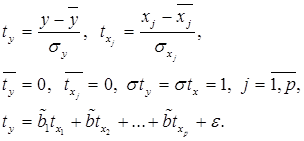
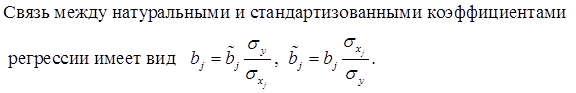
Долю влияния j–го фактора в суммарном влиянии всех факторов можно оценить по величине дельта–коэффициентов :

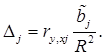
Качество уравнения множественной регрессии можно оценить с помощью коэффициента множественной корреляции или его квадрата – коэффициента детерминации

Если число наблюдений n недостаточно велико по сравнению с количеством факторов p, то величина R2 считается завышенной, и в таких случаях вычисляют исправленное значение R2.

.