После того как уравнение линейной регрессии построено, производится оценка значимости уравнения в целом и отдельных его параметров.

Значимость уравнения в целом оценивается по значению (величине) F–стати­стики Фишера. При этом выдвигается основная гипотеза о том, что коэффициент регрессии b равен нулю и фактор X не влияет на результат Y.

Для расчёта F используют дисперсии на одну степень свободы; такие диспер­сии сравнимы между собой по величине, так как приведены к общей шкале.

df – число степеней свободы (degrees of freedom),

df TSS = n­­­­–1, то есть свободно могут варьироваться n–1 отклонений, а n-е отклонение может быть вычислено по этим отклонениям и среднему значению

При заданном объёме наблюдений величина RSS в парной регрессии зависит от одной константы, а именно от коэффициента регрессии b, то есть RSS имеет одну степень свободы.

Дисперсии на одну степень свободы для парной регрессии обозначаются так:

По таблице Фишера–Снедекора, содержащей критические значения F при раз­ных уровнях γ существенности нулевой гипотезы и разных df, найдём Fкр (критическое значение) для конкретной задачи:

Если расчётное значение F >Fкр, то H0 отклоняется и связь между X и Y призна­ётся существенной, а уравнение признается адекватным. Если F < < < Fкр, то уравнение признается неадекватным.

В линейной регрессионной модели оценивают значимость не только уравнения в целом, но и отдельных его параметров. Для этого вначале определяются их стан­дартные ошибки: Sa, Sb, Sr.

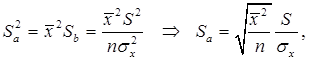
Имея в распоряжении величины a, b, rxy и их стандартные ошибки, можно вычислить t–статистики Стьюдента для оценки значимости этих параметров.

Выдвигается гипотеза H0 о незначимости интересующего коэффициента регрессии. Если , то гипотеза H0 не отклоняется, в противном случае она отклоняется и соответствующий коэффициент признается значимым.

На практике для приближенной оценки руководствуются следующим правилом:

– параметр значимым не признается, так как доверительная вероятность < 0,7;

– оценка параметра относительно значима и доверительная вероятность находится в пределах 0,7 0,95;

– оценка значима и доверительная вероятность находится в пределах 0,95 0,99;

– оценка гарантированно значима.

Эти правила хорошо работают при числе наблюдений больше десяти.